David Yates.
Advent of Code is a yearly programming event. For the 2024 edition, I decided to complete each challenge in a different language. After trying a lot of different language paradigms over the last two parts of this series, from rules-based to functional to logic to array, this next part represents something of a comedown. All of the languages I used for these five days were some flavour of imperative, and most were languages I’ve used before.
2D grid puzzles are a recurring theme this year, and I took the opportunity to use some gamedev frameworks for a couple of the challenges below.
# Day 11: Rust
Challenge: iterate over a list according to a set of rules and see how long it gets.
This was a deceptively simple challenge. You’re given a starting list containing two integers and a set of three rules for producing a new list. Two of the rules increase the integer, and the other rule splits it into two elements.
I’ve been using Rust quite a bit lately for non-AoC reasons, so I had to fit it in somewhere and this seemed like as good a place as any. The first part of the challenge was a simple matter of implementing the rules as described, which Rust’s match statement was well-suited for.
for _ in 0..blinks {
let mut new_stones = Vec::new();
for stone in stones {
match stone {
// 0 -> 1
0 => {
new_stones.push(1);
}
// even-length number -> split in half
n if n.to_string().len() % 2 == 0 => {
let s = stone.to_string();
let (first, second) = s.split_at(s.len() / 2);
new_stones.push(first.parse::<u64>().unwrap());
new_stones.push(second.parse::<u64>().unwrap());
}
// all else -> multiply by 2024
_ => {
new_stones.push(stone * 2024);
}
}
}
stones = new_stones;
}
println!("{:?} stones", stones.len());
Full code for part 1 on GitHub.
The first part was simple and the second part was deceptive. All that was required in the second part was to up the iteration count from 25 to 75. However, while the code produced an answer for 25 iterations pretty much instantly, it was not up to task of doing 75 with any reasonable amount of memory or time.
The example input showed that some of the elements repeated, so the first change I made was to create a cache hash map that would store the next iteration for each number after calculating it.
let mut cache: HashMap<u64, Vec<u64>> = HashMap::new();
for _ in 0..blinks {
let mut new_stones = Vec::new();
for stone in stones {
let mut added: Vec<u64> = Vec::new();
match stone {
// get from cache
n if cache.contains_key(&n) => {
added.extend(cache[&n].clone());
}
// 0 -> 1
0 => {
added.push(1);
}
// even-length number -> split in half
n if n.to_string().len() % 2 == 0 => {
let s = stone.to_string();
let (first, second) = s.split_at(s.len() / 2);
added.push(first.parse::<u64>().unwrap());
added.push(second.parse::<u64>().unwrap());
}
// all else -> multiply by 2024
_ => {
added.push(stone * 2024);
}
}
}
// add to stones
for &n in &added {
*stones.entry(n).or_insert(0) += count;
}
// add to cache
if !cache.contains_key(&stone) {
cache.insert(stone, added);
}
}
println!("{:?} stones", stones.len());
This didn’t help all that much. I thought about the problem some more, and realise that I would still end up building a really long list. Seeing as there were going to be a bunch of repeated elements, to the point where I was caching them, wouldn’t it make more sense to store the list as a hash map of unique elements with their counts? The order of the elements didn’t matter for either the iterations or the solution. So that’s what I did.
for (stone, count) in old_stones {
let mut added: Vec<u64> = Vec::new();
match stone {
// get from cache
n if cache.contains_key(&n) => {
added.extend(cache[&n].clone());
}
// 0 -> 1
0 => {
added.push(1);
}
// even-length number -> split in half
n if n.to_string().len() % 2 == 0 => {
let s = stone.to_string();
let (first, second) = s.split_at(s.len() / 2);
added.push(first.parse::<u64>().unwrap());
added.push(second.parse::<u64>().unwrap());
}
// all else -> multiply by 2024
_ => {
added.push(stone * 2024);
}
}
// add to stones
for &n in &added {
*stones.entry(n).or_insert(0) += count;
}
// add to cache
if !cache.contains_key(&stone) {
cache.insert(stone, added);
}
}
}
println!("{:?} stones", stones.values().sum::<u64>());
This implementation produced a result for 75 iterations pretty much instantly.
Full code for part 2 on GitHub.
Closing thoughts: The first time I looked at Rust, I came away scratching my head at all the crazy symbols and blocks everywhere. “What the hell is &mut?” I asked. Having now spent some time going through the official tutorial, working with some Rust codebases, and asking Claude about the weirder-looking bits of code I encounter, I’ve come to have quite an appreciation for the language. I’ve always been a big switch-case appreciator, so Rust’s match is something I like a lot. Having such expressive syntax and functional-type built-ins like map and fold in a fast, compiled language feels like cheating.
All that said, I intentionally avoided writing functions in this code so as not to have to think too much about ownership, which I don’t really have an intuition for yet.
# Day 12: C
Challenge: figure out the areas and perimeters of interlocking fields in a 2D grid.
After the previous day’s challenge, it was time to shake off all that rust (memory safety) and work in venerable old C.
Reading in the input file (a grid of characters) was a lot more manual than in higher-level languages, but it’s good to be reminded of such things now and then.
// Read garden map
rows = 0;
cols = 0;
char line[MAX_COLS];
while (fgets(line, sizeof(line), file) && rows < MAX_ROWS) {
// Remove newline if present
size_t len = strlen(line);
if (len > 0 && line[len-1] == '\n') {
line[len-1] = '\0';
len--;
}
// Skip empty lines
if (len == 0) continue;
// Set cols based on first line
if (rows == 0) {
cols = len;
} else if (len != cols) {
printf("Inconsistent line length at row %d\n. Expected %d, got %d", rows, cols, len);
fclose(file);
return 1;
}
for (size_t i = 0; i < len; i++) {
garden[rows][i] = line[i];
}
garden[rows][len] = '\0';
rows++;
}
fclose(file);
To calculate the areas and perimeters of interlocking fields, I did a depth-first search on the grid.
// DFS to calculate area and perimeter of a region
void calculate(int r, int c, char plant_type, int *area, int *perimeter, int *corners) {
visited[r][c] = true;
(*area)++;
// Count perimeter edges
for (int i = 0; i < 4; i++) {
int nr = r + dr[i];
int nc = c + dc[i];
if (nr < 0 || nr >= rows || nc < 0 || nc >= cols || garden[nr][nc] != plant_type) {
(*perimeter)++;
} else if (!visited[nr][nc]) {
calculate(nr, nc, plant_type, area, perimeter, corners);
}
}
}
The final result was the sum of the area times the perimeter of each region. So far, so simple.
For the second part of the challenge, it was necessary to figure out how many sides each region had.
AAA
AAA --> four sides
AAA
BBB
BBBB --> six sides
BBBB
Counting sides seemed kind of tricky. Counting corners was a lot easier, and would produce the same result, so I did that. The following function checks for corners by looking at the contents of the three cells around the target cell in each of the four cardinal directions.
// Count corners at a given cell
int count_corners(int r, int c, char plant_type) {
int corners = 0;
// Check if we have a corner in each of the 4 quadrants around this cell
for (int i = 0; i < 4; i++) {
// Get coordinates for the three cells we need to check
int r1 = r + dr[i];
int c1 = c + dc[i];
int r2 = r + dr[(i+1)%4];
int c2 = c + dc[(i+1)%4];
int rd = r + dr[i] + dr[(i+1)%4];
int cd = c + dc[i] + dc[(i+1)%4];
// Inner corner if both adjacent cells are the same type
// and the diagonal is different
if (r1 >= 0 && r1 < rows && c1 >= 0 && c1 < cols &&
r2 >= 0 && r2 < rows && c2 >= 0 && c2 < cols &&
rd >= 0 && rd < rows && cd >= 0 && cd < cols &&
garden[r1][c1] == plant_type &&
garden[r2][c2] == plant_type &&
garden[rd][cd] != plant_type) {
corners++;
continue;
}
// Outer corner if either adjacent cell is out of bounds or different type
bool cell1_different = (r1 < 0 || r1 >= rows ||
c1 < 0 || c1 >= cols || garden[r1][c1] != plant_type);
bool cell2_different = (r2 < 0 || r2 >= rows ||
c2 < 0 || c2 >= cols || garden[r2][c2] != plant_type);
if (cell1_different && cell2_different) {
corners++;
}
}
return corners;
}
Closing thoughts: The only times when I really felt like I was writing in C was when I was checking for null bytes at the end of strings and passing pointers around. When working on the core of the puzzle, depth-first search and 2D grid navigation I felt like I could have been working in just about any language. Which I suppose is further evidence of C’s long shadow.
# Day 13: Octave
Challenge: find the right moves to win the prizes in a bunch of claw machines.
For this challenge, each claw machine has a single prize and two buttons. Each button moves the claw some distance along the X and Y axes. Button A costs three tokens and B costs one. You need to figure out the right number of times to press each button to reach the prize with minimum expenditure. Some of the machines are broken and have no solution.
After a little thinking, this challenge reveals itself to be a highschool algebra problem: each machine is a set of simultaneous equations. So this:
Button A: X+94, Y+34
Button B: X+22, Y+67
Prize: X=8400, Y=5400
Becomes this:
94a + 22b = 8400
34a + 67b = 5400
It therefore seemed appropriate to use a maths language. Matlab and Mathematica come most easily to mind, but both are proprietary and costly, so I went with GNU Octave.
pkg load symbolic
% Open the file and read the entire content
fileID = fopen('input.txt', 'r');
fileContent = fread(fileID, '*char')';
% ^ unmatched ' is transpose -- necessary to read file as lines rather than columns
fclose(fileID);
% Split the content into blocks
blocks = strsplit(fileContent, '\n\n');
% Initialize sums for A and B
sumA = 0;
sumB = 0;
% Process each block
for i = 1:length(blocks)
lines = strsplit(strtrim(blocks{i}), '\n');
% Extract numbers from the strings
buttonA_nums = sscanf(lines{1}, 'Button A: X+%d, Y+%d');
buttonB_nums = sscanf(lines{2}, 'Button B: X+%d, Y+%d');
prize_nums = sscanf(lines{3}, 'Prize: X=%d, Y=%d');
% Build the equations
syms A B
eq1 = A*buttonA_nums(1) + B*buttonB_nums(1) == prize_nums(1);
eq2 = A*buttonA_nums(2) + B*buttonB_nums(2) == prize_nums(2);
% Solve the equations (hardest part of the challenge in one built-in function)
sol = solve([eq1, eq2], [A, B]);
% Discard non-integer solutions
if mod(sol.A, 1) == 0
sumA = sumA + double(sol.A);
end
if mod(sol.B, 1) == 0
sumB = sumB + double(sol.B);
end
end
% Display the summed results
disp(sumA*3 + sumB);
Full code for part 1 on GitHub.
The second part of the challenge, explicitly designed for people like me, required the addition of 10 000 000 000 000 (ten trillion) to each prize co-ordinate. This was enough to make all co-ordinates significantly larger than the largest 32-bit integer – Octave’s default integer type. After converting all of my numbers to int64, I got a punch of precision errors. Following a bunch of fiddling with stubbornly broken code, I took a step back and asked what other ways there might be to solve simultaneous equations.
Cramer’s rule was not something I remembered from highschool algebra, but it was pretty simple to implement.
% Open the file and read the entire content
fileID = fopen('input.txt', 'r');
fileContent = fread(fileID, '*char')';
% ^ unmatched ' is transpose -- necessary to read file as lines rather than columns
fclose(fileID);
% Split the content into blocks
blocks = strsplit(fileContent, '\n\n');
% Initialize sums for A and B
sumA = int64(0);
sumB = int64(0);
% Process each block
for i = 1:length(blocks)
lines = strsplit(strtrim(blocks{i}), '\n');
% Extract numbers from the strings and convert to int64
buttonA_nums = int64(sscanf(lines{1}, 'Button A: X+%d, Y+%d'));
buttonB_nums = int64(sscanf(lines{2}, 'Button B: X+%d, Y+%d'));
prize_nums = int64(sscanf(lines{3}, 'Prize: X=%d, Y=%d'));
% Add the large number
prize_nums = prize_nums + int64(10000000000000);
% Build the Cramer equations
a1 = buttonA_nums(1); a2 = buttonA_nums(2);
b1 = buttonB_nums(1); b2 = buttonB_nums(2);
c1 = prize_nums(1); c2 = prize_nums(2);
% Calculate determinants
D = a1 * b2 - a2 * b1;
Dx = c1 * b2 - c2 * b1;
Dy = a1 * c2 - a2 * c1;
% Discard non-integer solutions
if D ~= 0
x = Dx / D;
y = Dy / D;
if mod(Dx, D) == 0 && mod(Dy, D) == 0
sumA = sumA + x;
sumB = sumB + y;
end
end
end
% Display the summed results
result = sumA * int64(3) + sumB;
disp(result);
Full code for part 2 on GitHub.
Closing thoughts: This was a place where the features of the language really came through for solving the challenge, to the point where the first part was really just a matter of string parsing and calling solve. I suppose the real trick was to figure out that you needed to use simultaneous equations.
I found Octave fairly simple to use, but in the usual course I would probably just do this sort of thing in Python. Octave’s symbolic package, which I used for the first part of the challenge, is largely a wrapper for SymPy.
# Day 14: Lua & Love2D
Challenge: simulate guard robot movements.
Lua was one of the languages on my shortlist for this challenge. My main previous experience with it was writing LuaLaTeX in Overleaf to create dynamic document templates – aside from that, I’d occasionally tinkered with Love2D, a Lua-based gamedev framework. A challenge involving guard robots moving through a 2D grid seemed like a good opportunity to bring in not only Lua, but Love2D.
Implementing the guard simulation in Love2D was pretty straightforward, but to actually solve the challenge you need pretty discrete results – which robots are in which grid spaces at precise times. Love2D is geared to show fluid movement in real-time, and getting it to do otherwise made me feel like I was fighting with my code. So I retreated to a pure Lua solution based on the text grid.
local function moveGuards(guards, mapWidth, mapHeight)
for _, guard in ipairs(guards) do
guard.x = guard.x + guard.vx
guard.y = guard.y + guard.vy
-- wrap at the edges
if guard.x < 1 then
guard.x = guard.x + mapWidth
elseif guard.x > mapWidth then
guard.x = guard.x - mapWidth
end
if guard.y < 1 then
guard.y = guard.y + mapHeight
elseif guard.y > mapHeight then
guard.y = guard.y - mapHeight
end
end
end
local function calculateSafety(guards, mapWidth, mapHeight)
local quadrants = {0, 0, 0, 0}
local centerX = math.ceil(mapWidth / 2)
local centerY = math.ceil(mapHeight / 2)
-- Count robots in each quadrant
for _, guard in ipairs(guards) do
-- Skip robots exactly on center lines
if guard.x == centerX or guard.y == centerY then
goto continue -- Lua has no continue statement
end
-- Count each quadrant
if guard.y < centerY then
if guard.x < centerX then
quadrants[1] = quadrants[1] + 1 -- Top-left
elseif guard.x > centerX then
quadrants[2] = quadrants[2] + 1 -- Top-right
end
elseif guard.y > centerY then
if guard.x < centerX then
quadrants[3] = quadrants[3] + 1 -- Bottom-left
elseif guard.x > centerX then
quadrants[4] = quadrants[4] + 1 -- Bottom-right
end
end
::continue:: -- We jump here (poor man's continue)
end
return quadrants[1] * quadrants[2] * quadrants[3] * quadrants[4]
end
local file = io.open("input.txt", "r")
local guards = {}
for line in file:lines() do
local startX, startY, vx, vy = line:match("p=(%d+),(%d+) v=(%-?%d+),(%-?%d+)")
-- ^ I can't believe it's not regex!
table.insert(guards, {
x = tonumber(startX+1), -- +1 to account for Lua's 1-based indexing
y = tonumber(startY+1), -- +1 to account for Lua's 1-based indexing
vx = tonumber(vx),
vy = tonumber(vy),
})
end
file:close()
local mapWidth = 101
local mapHeight = 103
for i = 1, 100 do
moveGuards(guards, mapWidth, mapHeight)
end
print(calculateSafety(guards, mapWidth, mapHeight))
A few notes:
- I learnt about Lua’s pattern matching doing this challenge. It is not regex, as implementing regex in Lua would practically double the size of its codebase. Luckily, I didn’t need to do any complicated text parsing for this challenge. This cheatsheet was helpful.
line:matchis syntactic sugar forline.match(self,. I had also not previously used any of Lua’s OO capabilities.- Lua 1-indexes everything (as does Octave).
Naturally, this code got me a result much quicker than my Love2D implementation.
Full code for part 1 on GitHub
The second part of the challenge comes totally out of left field: you have to find the smallest number of seconds it takes for the robots to arrange themselves in a Christmas tree pattern. I immediately had more questions, such as, should this be an actual tree or something in vague shape of one? At any rate, solving this problem with my current implementation would require a function for visualising the map:
local function visualizeMap(guards, mapWidth, mapHeight)
-- Initialize empty map
local map = {}
for y = 1, mapHeight do
map[y] = {}
for x = 1, mapWidth do
map[y][x] = 0
end
end
-- Count guards at each position
for _, guard in ipairs(guards) do
local x, y = math.floor(guard.x), math.floor(guard.y)
map[y][x] = map[y][x] + 1
end
-- Create string representation
local result = {}
for y = 1, mapHeight do
local row = {}
for x = 1, mapWidth do
row[x] = map[y][x] > 0 and tostring(map[y][x]) or "."
end
table.insert(result, table.concat(row))
end
return table.concat(result, "\n")
end
I didn’t have any idea what the eventual tree would look like, so I didn’t really want to try writing code to detect shapes in guard positions. Luckily, I still had my abandoned Love2D implementation, which I could start up and just watch for patterns.
I soon noticed that the guards would periodically swarm to the vertical or horizontal center line of the map. As these lines were left out of the safety factor calculation, this meant that such a swarm would have to coincide with a low safety factor. Also it would make sense for the Christmas tree to appear in the middle of the map.
Initially, I tried looking for the lowest possible safety factor in a hundred, then one thousand, then ten thousand seconds. Although I could lie to myself that some of these outputs looked vaguely like Christmas trees, none were the correct answer. So I loosened my threshold a bit, and looked for outputs with safety factors lower than the first one I found, at the first second I’d noticed the middle convergence.
A few results down, I saw this, right in the centre of the map:
1111111111111111111111111111111
1.............................1
1.............................1
1.............................1
1.............................1
1..............1..............1
1.............111.............1
1............11111............1
1...........1111111...........1
1..........111111111..........1
1............11111............1
1...........1111111...........1
1..........111111111..........1
1.........11111111111.........1
1........1111111111111........1
1..........111111111..........1
1.........11111111111.........1
1........1111111111111........1
1.......111111111111111.......1
1......11111111111111111......1
1........1111111111111........1
1.......111111111111111.......1
1......11111111111111111......1
1.....1111111111111111111.....1
1....111111111111111111111....1
1.............111.............1
1.............111.............1
1.............111.............1
1.............................1
1.............................1
1.............................1
1.............................1
1111111111111111111111111111111
As we can see, none of the guards overlap in this pattern. That would probably also be a good heuristic for finding the Christmas tree, but I haven’t implemented it.
Full code for part 2 on GitHub.
After implementing some time manipulation functionality in my Love2D code, I managed to snap a screenshot of it as well.
Merry Christmas!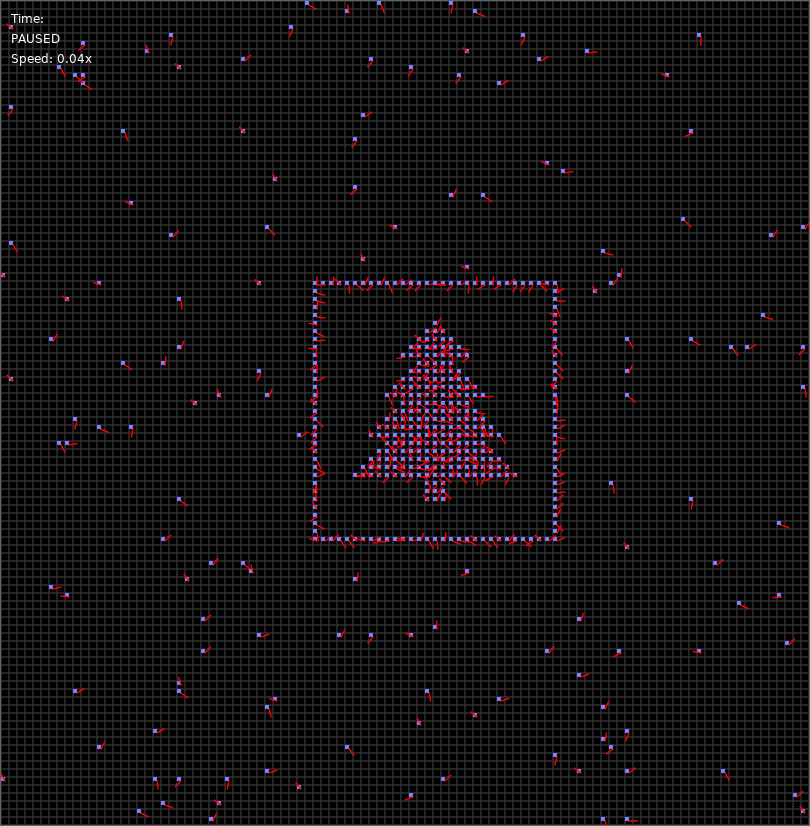
Full code for Love2D version on GitHub.
Closing thoughts: I think if I could get used to 1-indexing, I’d probably prefer it to 0-indexing. Sacrilege, I know. Lua is a great little language and I’m glad I used this opportunity to get a bit more experience with it and learn about things like its pattern-matching functionality.
Love2D is great fun, and I’m glad that my failed Love2D implementation of the first part of the challenge turned out to be useful for the second part.
# Day 15: JavaScript & KaPlay
Challenge: figure out where a malfunctioning robot will push boxes in a warehouse.
The challenge here was to build a self-playing sokoban game, making it the challenge most perfectly suited so far to a gamedev framework.1
Initially, I thought about using PuzzleScript, a gamedev tool with a terse, rule-based language explicitly geared to the creation of sokoban-alikes. Half of the logic for the first part of this challenge is already implemented in the sample game, in a single line of code:
[ > Player | Crate ] -> [ > Player | > Crate ]
Translation: if player steps towards a crate, move both the player and the crate. To complete the logic, we just need to make crates push each other, which we can do with another very simple rule:
[ > Crate | Crate ] -> [ > Crate | > Crate ]
However, getting a result out of a PuzzleScript game would require some external method of:
- Moving the player according to a preset list of moves.
- Calculating and adding the positions of all the crates together.
This seemed like a lot more trouble than it was worth, even in the context of this self-imposed challenge. So I opted instead to write my self-playing sokoban game in JavaScript, using KaPlay, a lightweight and intuitive gamedev library I have a bit of prior experience with. KaPlay also happens to have functionality for storing levels as ASCII grids, making it well suited to AoC.
After creating a new project, loading up some sprites and making a sample level using 16x16 grid spaces, to semi-accomodate the large challenge input, I got to work with my implementation. Initially, I wrote a bunch of code for predicting which object(s) the player would collide with when moving in some direction, converting between real positions and grid positions, but then I realised that at some point since I last used it, KaPlay had added the method level.getAt which did all of this for me. That allowed me to implemented the movement and crate-pushing code in a few recursive functions.
// Base movement function
const move = (obj, dir) => {
if (dir.x == 1) obj.moveRight();
if (dir.x == -1) obj.moveLeft();
if (dir.y == 1) obj.moveDown();
if (dir.y == -1) obj.moveUp();
};
// Crate movement
const moveCrate = (crate, dir) => {
const crateMoveTo = crate.tilePos.add(dir);
const crateDisplaced = level.getAt(crateMoveTo)[0];
// ^ multiple objects could occupy the same grid space
// but that shouldn't happen in this game
// Moving into empty space: success
if (crateDisplaced === undefined) {
move(crate, dir);
return true;
}
// Moving into a wall: failure
if (crateDisplaced.is("wall")) {
return false;
}
// Moving into another crate: pass the buck
if (crateDisplaced.is("crate")) {
const nextCrate = crateDisplaced;
if (moveCrate(nextCrate, dir)) {
move(crate, dir);
return true;
}
return false;
}
}
// Player movement
const movePlayer = (dir) => {
const moveTo = player.tilePos.add(dir);
const displaced = level.getAt(moveTo)[0];
// Moving into empty space
if (displaced === undefined) {
move(player, dir);
return;
}
// Moving into a wall, cancel movement
if (displaced.is("wall")) {
return;
}
// Moving into a crate, try to push the crate
if (displaced.is("crate")) {
const crate = displaced;
if (!moveCrate(crate, dir)) {
return;
}
}
// If we haven't returned yet, we can move
move(player, dir);
};
For testing, and to make it a real game, I bound movement to the arrow keys. I then implemented autoplay in two ways. Press Space, and all moves will be processed at once, changing the map and producing the answer in the blink of an eye. Press Enter, and you can watch the robot go through the moves one at a time.
Sokoban, featuring Bean, the default KaPlay player sprite
For the second part of the challenge, everything except the player/robot doubled in width, taking up two grid spaces. At this point, I regretted using GML back on day four, as GameMaker’s collision and grid functions are robust enough to handle this kind of thing with ease. Had I implemented part one in GameMaker, I would likely only have to have changed the width of the crates to get part two working as well. However, I implemented it in KaPlay. And KaPlay’s level/tile system does not explicitly for cater double-wide objects. I would either have forgo a lot of the tile functionality or work with left and right crate halves, which would need to be manually kept together.
The only real challenge was keeping crates together when they were pushed vertically. Due to the cascading push already implemented for part 1, horizontally pushing two separate crates positioned next to each other was functionally the same as pushing two linked crates. It was when crates had to be pushed vertically that the difficulty in keeping halves together came in.
I tried a few different tweaks to my recursive code above, but couldn’t resolve this edge-case:
Pushing up… Telepathic push
Annoyingly, this edge-case was not present in the example map, but did appear in my challenge input. All of my recursive methods were just too eager to move boxes. I needed to move to something that would cancel the whole move as soon as one move failed.
So, taking a leaf from challenges 10 and 12, I rewrote the code to build up an array of things to move using a depth-first search.
const movePlayer = (dir) => {
const moveTo = player.tilePos.add(dir);
let displaced = level.getAt(moveTo)[0];
// empty space, go there
if (displaced === undefined) {
move(player, dir);
return;
}
// wall, don't go there
if (displaced.is("wall")) {
return;
}
// not empty space or wall, must be a crate
// let's build a stack of crates in our way
let cratesToMove = new Set();
let stack = [displaced];
while(stack.length > 0) {
let next = stack.pop();
if (next) {
if (next.is("wall")) return; // found a wall, cancel everything
if (next.is("crate")) {
// add to crates to move
cratesToMove.add(next);
// add to displacement checking stack
stack.push(level.getAt(next.tilePos.add(dir))[0]);
}
if (dir.y != 0) { // special rules for vertical movement
// partner crate must also be able to move
if (next.is("left")) {
let partner = level.getAt(next.tilePos.add(vec2(1, 0)))[0]
cratesToMove.add(partner);
stack.push(level.getAt(partner.tilePos.add(dir))[0]);
}
if (next.is("right")) {
let partner = level.getAt(next.tilePos.add(vec2(-1, 0)))[0]
cratesToMove.add(partner);
stack.push(level.getAt(partner.tilePos.add(dir))[0]);
}
}
}
}
// move everything that needs to move
for (const crate of cratesToMove) {
move(crate, dir);
}
move(player, dir);
};
What I’m happiest about with this code is that it works just as well for single and double-sized crates, and thus works as a solution for both parts of the challenge. It would also work on a map including a mix of short and long crates. To facilitate solving this part two, I added an upsize checkbox to the functionality that loads levels from files, and that’s all I needed.
Double-width Sokoban
Closing thoughts: I have never been the biggest fan of JavaScript, but it’s one of those languages that you pretty much have no choice but to use in a lot of domains. As a result, I’m very comfortable with it, which has not been the case for most of what I’ve used for these challenges.
KaPlay is a great little library and one I’d like to use for a proper game in the future.
As may be evident from the date of this compared to previous posts, I’ve slowed down with this project a little. Write-ups for the remaining ten days of AoC 2024 will be posted eventually, probably with some other posts in between. I feel like I played it quite safe with the language choices for this selection of challenges, so I’m looking forward to trying some weirder ones in the next post.
-
One person went even further than this and implemented it in the meta-sokoban game Baba is You. ↩︎